坐标投影变换

我们知道地球是一个球体，而我们平常所用的地图则都是平面图。这就以为着存在着某种变换，将我们的地球通过这种变换最终投影形成我们平常所用的投影。在这里，我们将介绍一个叫做“墨卡托”投影的方法，这种投影方法目前广泛应用在各大在线地图厂商之中，同时在航海等领域也有着广泛的应用。

墨卡托投影法

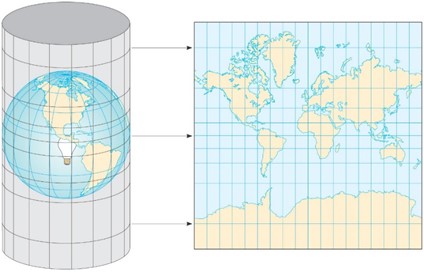
麦卡托投影法(Mercator projection)，是一种等角的圆柱形地图投影法。本投影法得名于杰拉杜斯·麦卡托，法兰提斯出身的地理学家、地图学家。他于1569年发表长202公分、宽124公分以此方式绘制的世界地图。在以此投影法绘制的地图上，经纬线于任何位置皆垂直相交，使世界地图可以绘制在一个长方形上。由于可显示任两点间的正确方位，航海用途的海图、航路图大都以此方式绘制。在该投影中线型比例尺在图中任意一点周围都保持不变，从而可以保持大陆轮廓投影后的角度和形状不变（即等角）；但麦卡托投影会使面积产生变形，极点的比例甚至达到了无穷大。
简单来说，墨卡托投影就是以地球球心为出发点，将地球投影到一个与地球赤道相切的圆柱体之上，再将圆柱体展开即形成了投影后的地图。从投影原理我们可以看出，墨卡托投影具有“等角”的特性，也就是说经过投影之后的地图形状保持不变。
由此原理，我们就可以推出地理坐标与墨卡托投影坐标之间的转换关系。简单来说，投影坐标系(PROJCS)是平面坐标系，以米为单位；而地理坐标系(GEOGCS)是椭球面坐标系，以经纬度为单位。经度：这边没问题，可取全球范围：[-180,180]。 纬度：上面已知，纬度不可能到达90°，懒人们为了正方形而取的-20037508.3427892，经过反计算，可得到纬度85.05112877980659。因此纬度取值范围是[-85.05112877980659，85.05112877980659]。也就是说经过投影之后的地图纬度范围并不能达到两个极点，不过这对我们日常使用几乎没有影响。

墨卡托变换公式

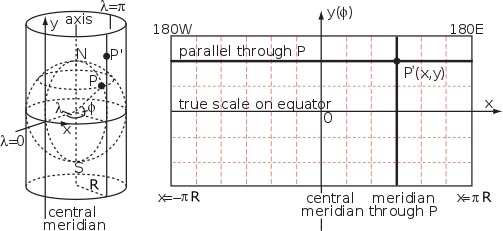
从图中我们可以得出以下的转换公式：
$\lambda=x$
$\psi=2\cdotp\arctan{e^y}-\frac{\pi}{2}$

$x=\lambda$
$y=\ln{\tan{\psi}+\sec{\psi}}$